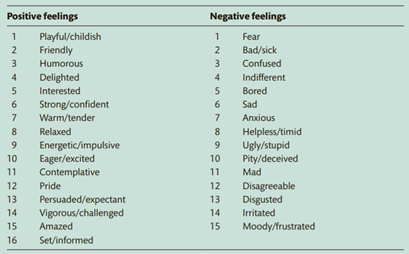
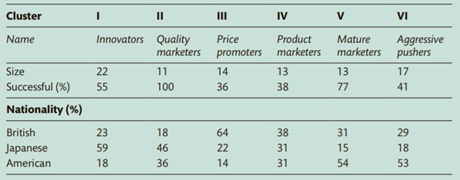
solution

/in /by

Ice cream ‘hot spots

Häagen-Dazs Shoppe Co. (www.haagendazs.com), with more than 850 retail ice cream shops in over 50 countries, was interested in expanding its customer base. The objective was to identify potential consumer segments that could generate additional sales. It used geodemographic techniques (as discussed in Chapter 5), which are based upon clustering consumers using geographic, demographic and lifestyle data. Additional primary data were collected to develop an understanding of the demographic, lifestyle and behavioural characteristics of Häagen-Dazs Shoppe users, which included frequency of purchase, time of day to visit café, day of the week and a range of other product variables. The postcodes or zip codes of participants were also obtained. The participants were then assigned to 40 geodemographic clusters based upon a clustering procedure developed by Nielsen Claritas (www.nielsen.com). Häagen-Dazs compared its profile of customers with the profile of geodemographic classifications to develop a clearer picture of the types of consumer it was attracting. From this it decided which profiles of consumer or target markets it believed to hold the most potential for additional sales. New products were developed and advertising was established and profiled to target specific consumer types.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

Feelings – nothing more than feelings

As it faced stiff competition in digital cameras, Nikon (www.nikon.com) was marketing its Coolpix line with the tag lines ‘passion made powerful’, ‘brilliance made beautiful’ and ‘memories made easy’. The advertising campaign was designed to evoke emotional feelings in consumers. Nikon based this campaign on a study conducted to identify feelings that were intuitively evoked. A total of 655 feelings were reduced to a set of 180 that were judged by participants to be most likely to be stimulated by advertising. This group was clustered on the basis of judgements of similarity between feelings, resulting in 31 ‘feelings’ clusters. These were divided into 16 positive and 15 negative clusters, as shown in the table.

Thus, 655 feelings responses to advertising were reduced to a core set of 31 feelings. In this way, advertisers now have a manageable set of feelings for understanding and measuring responses to advertising. When measured, these feelings can provide information on a commercial’s ability to persuade target consumers, as in the case of Nikon cameras.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

Segmentation with surgical precision

Cluster analysis was used to classify and segment participants, based upon their preferences for hospitals that provide inpatient care. The clustering was based on the reasons participants gave for preferring a particular hospital. The demographic profiles of the grouped participants were compared to learn whether the segments could be identified more efficiently. The k-means clustering method (SPSS) was used for grouping the participants based on their answers to the hospital preference items. The squared Euclidean distances between all clustering variables were minimised. Because different individuals perceive scales of importance differently, each individual’s ratings were normalised before clustering. The results indicated that the participants could be best classified into four clusters. The cross-validation procedure for cluster analysis was run twice, on halves of the total sample. As expected, the four groups differed substantially by their distributions and average responses to the reasons for their hospital preferences. The names assigned to the four groups reflected the demographic characteristics and reasons for hospital preferences: ‘old-fashioned’, ‘affluent’, ‘value conscious’ and ‘professional want-it-alls’.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

It is a small world

Data for a study of British, Japanese and American competitors were obtained from detailed face-to-face interviews with chief executives and top marketing decision makers for defined product groups in 90 companies. To control for market differences, the methodology was based upon matching 30 British companies with their major Japanese and American competitors in the British market. The study involved 30 triads of companies, each composed of a British, Japanese and American business that competed directly with one another. Most of the data on the characteristics of the companies’ performance, strategy and organisation were collected on five-point semantic differential scales. The first stage of the analysis involved factor analysis of variables describing the firms’ strategies and marketing activities. The factor scores were used to identify groups of similar companies using Ward’s hierarchical clustering routine. A six-cluster solution was developed.

Membership in the six clusters was then interpreted against the original performance, strategy and organisational variables. All the clusters contained some successful companies, although some contained significantly more than others. The clusters lent support to the hypothesis that successful companies were similar irrespective of nationality, since British, Japanese and American companies were found in all the clusters. There was, however, a preponderance of Japanese companies in the more successful clusters and a predominance of British companies in the two least successful clusters. Apparently, Japanese companies did not deploy strategies that were unique to them; rather, more of them pursued strategies that worked effectively in the British market. The findings indicated that there were generic strategies that described successful companies, irrespective of their industry. Three successful strategies could be identified. The first was the quality marketing strategy. These companies had strengths in marketing and research and development. They concentrated their technical developments on achieving high quality rather than pure innovation. These companies were characterised by entrepreneurial organisations, long-range planning and a well-communicated sense of mission. The second generic strategy was that of the innovators, who were weaker on advanced research and development but were entrepreneurial and driven by a quest for innovation. The last successful group were the mature marketers, who were highly profit oriented and had in-depth marketing skills. All three appeared to consist of highly marketing-oriented businesses.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"