solution

/in /by

Juniper Networks to Benefit From Digital India Programme

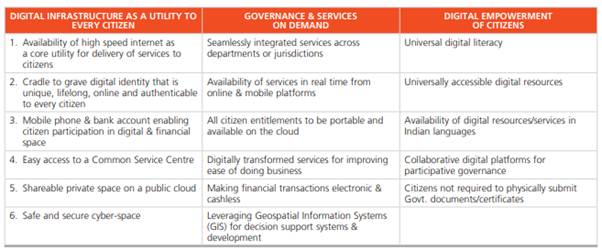
Juniper Networks is an American multinational corporation headquartered in Sunnyvale, California that develops and markets networking products. Its products include routers, switches, network management software, network security products and software-defined networking technology. Company competes with Cisco, Ciena and Hewlett-Packard, among others. The NYSE-listed company has invested $1 billion in India in the past six years, mostly on research and development, and has about 2,600 workers in the country across locations including Bengaluru and Delhi. Juniper Networks is planning to invest $1 billion more in the Indian operations to tap into the opportunities which will arise from India’s digital transformation led by cloud-based services. The company wants to be part of Government of India’s digital vision. The Digital India programme is centred on three key vision areas:

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

1. You are engaged in active listening with a colleague. you note though that the speaker’s body language is sending a different message than the words you are hearing. What do you do?

2. Your team has selected a course of action and are about to implement it. One of your employees shows you a memo with the identical solution your team has selected. It’s dated 2015. “What happened?”, you ask him. “We agreed on it, then we got busy with other stuff, and just never got around to implementing”, he says.

How do you make sure your solution is implemented, accepted, and watched over until it becomes routine?

Please be a gem and answer each which 4-5 sentences please super appreciative nothing crazy.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

A literature review is important in more ways than one, it’s similar to asking the question, why is sleeping, eating and exercising, important! Ok, that may be different and it’s not the best comparison but you get the point! You need all of them to function, support your system, provide nutrients and feed your brain to help you understand and retain as much information as you can possibly can! A literature review is important because it supports your findings, helps demonstrate an understanding of your research/topic, and to justify your research. Mentioned in an article was, “The aim of any literature review is to summarize and synthesize the arguments and ideas of existing knowledge in a particular field without adding any new contributions.”(pubrica, 2019). You can write about a topic without knowing about the topic right, it’s like the blind leading the blind. You must have at least a general understanding of the topic or argument to start and get a feel of the direction you would like to go in and this way the research part comes fairly easy. You’ll know what to look for, where you want to focus and how you want to approach the review.

Would you agree with the writer?Why or Why not? What other reasons may a literature review be important?

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by
A campus wireless installation project costs GH¢ 36,000 and is expected to generate cash inflows of 11,200 annually for five years. Calculate the IRR. Your company has been presented with a new proposal to develop a new school management system. The cost of the project development is $500,000. The probability of successful development is projected to be 70%. If the development is unsuccessful, the project will be terminated. If it is successful, the developer must then decide whether to begin developing a completely new school management system or modify an existing school management system. If the demand for the new school management system is high, the incremental revenue for the school management system is $1,200,000, and the incremental revenue for the modified school management system is $850,000. If the demand is low, the incremental revenue for the new school management system is $700,000, and the incremental revenue for the modified school management system is $720,000. All of these incremental revenue values are gross figures, i.e., before subtracting the $500,000 development cost, $300,000 for the new school management system and $100,000 for the modified school management system. The probability of high demand is estimated as 40%, and of low demand as 60%.
 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"