solution

/in /by

Harmel et al. [2006] compiled a cross-system data set to study the effects of agriculture activities on water quality. The data included in the study were mostly field scale experiments that measured nutrients (P, N) loading leaving a field. The data set (agWQdata.csv) includes the measured TP loading (TPLoad, in kg/ha), land use (LU), tillage method (Tillage), and fertilizer application methods (FAppMethd). You are to determine whether tillage methods affect TP loading.

(a) Estimate the mean TP loading for each tillage method (an easy way to do this in R is to use the function tapply):

Harmel et al. [2006] compiled a cross-system data set to study the effects of agriculture activities...

(b) Discuss briefly whether logarithm transformation is necessary.

(c) Use statistical test to study whether different tillage methods resulted in different TP loading (state the null and alternative hypothesis, conduct the test, report the result).

(d) Discuss briefly how useful is the test result.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

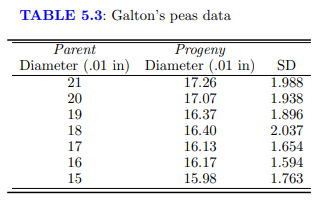
Huey et al. [2000] studied the development of a fly (Drosophila subobscura) that had accidentally been introduced from Europe (EU) into North America (N.A.) around 1980. In Europe, characteristics of the flies’ wings follow a “cline” – a steady change with latitude. One decade after introduction, the N.A. population had spread throughout the continent, but no such cline could be found. After two decades, Huey and his team collected flies from 11 locations in western N.A. and native flies from 10 locations in EU at latitudes ranging from 35 to 55 degrees N. They maintained all samples in uniform conditions through several generations to isolate genetic differences from environmental differences. Then they measured about 20 adults from each group. The data set flies.txt shows average wing size in millimeters on a logarithmic scale.

(a) In their paper, Huey et al. used four separate regression models to suggest that female flies from both EU and N.A. have the same wing length – latitude relationship (identical slopes), while the same relationships for male flies from the two continent are close but they were unable to say whether the slopes are the same.

We know that we can create a categorical variable to identify a fly’s origin and sex. This variable can be created by pasting the columns Continent and Sex:

Huey et al. [2000] studied the development of a fly (Drosophila subobscura) that had accidentally...-1

we obtain a model with four intercepts and four slopes, and the intercept and slope for the first level of FlyID (sorted alphabetically) is estimated and presented as the baseline.

Fit the linear model and interpret the results. Compare your results to the results presented in Huey et al. [2000]. Comment on any differences and why you feel you should use the approach we used here.

(b) The model we fitted here has its limitation. Only the slope and intercept of the first level are presented in the results explicitly. In this case, we will only see the intercept and slope for Female.EU, the baseline. Intercepts and slopes for the other three levels are presented in terms of their differences from the baseline. This is set up for hypothesis testing. That is, we can compare whether the slopes for Female.N.A., Male.EU, Male.N.A. are different from the slope for Female.EU. For this particular model, we can directly test whether the difference in slope between Female.EU and the slope of Female.N.A. is different from 0, but we cannot directly compare the slopes and intercepts for Male.EU and Male.N.A. To make this comparison, we must set Male.EU as the baseline first:

Huey et al. [2000] studied the development of a fly (Drosophila subobscura) that had accidentally...-2

which will change FlyID into a numeric variable with integers 1 to 4, and 1 is “Male.EU”, 2 is “Male.N.A.”, 3 is “Female.EU”, and 4 is “Female.N.A.”. Now refit the same model as in (a). Using results from both (a) and (b) to compare whether the slope for male flies from N.A. differs from the slope for male flies from EU, and whether the slope for female flies from N.A. differs from the slope for female flies from EU.

(c) In their paper, the linear regression models have very low R2 values, and the model we fit has a very high R2 value. Why? Is our model that much better?

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance of characteristics from one generation to the next. In a paper on “Typical Laws of Heredity,” delivered to the Royal Institution on February 9, 1877, Galton discussed some experiments on sweet peas. By comparing the sweet peas produced by parent plants to those produced by offspring plants, he could observe inheritance from one generation to the next. Galton categorized parent plants according to the typical diameter of the peas they produced. For seven size classes from 0.15 to 0.21 inches, he arranged for each of nine of his friends to grow 10 plants from seed in each size class; however, two of the crops were total failures. A summary of Galton’s data was published by Karl Pearson (see table 5.3 and the data file galtonpeas.txt). Only average diameters and standard deviation of the offspring peas are given by Pearson; sample sizes are unknown.

(a) Draw the scatter plot of Progeny versus Parent.

(b) Assuming that the standard deviations given are population values, compute the regression of Progeny on Parent and draw the fitted mean function on the scatter plot.

(c) Galton wanted to know if characteristics of the parent plant such as size were passed on to the offspring plants. In fitting the regression, a parameter value of Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-11 = 1 would correspond to perfect inheritance, while Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-11 Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-3 1 would suggest that the offspring are “reverting” towards “what may be roughly and perhaps fairly described as the average ancestral type” (the substitution of “regression” for “reversion” was probably due to Galton in 1885). Test the hypothesis that β1 = 1 versus the alternative that β1

(d) In his experiments, Galton took the average size of all peas produced by a plant to determine the size class of the parent plant. Yet for seeds to represent that plant and produce offspring, Galton chose seeds that were as close to the overall average size as possible. Thus, for a small plant, exceptionally large seed was chosen as a representative, while larger, more robust plants were represented by relatively smaller seeds. What effects would you expect these experimental biases to have on (1) estimation of the intercept and slope and (2) estimates of error?

table 5.3

Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-4

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

Logarithmic transformations: data set pollution.csv (variable definitions are in file pollution.txt) contains mortality rates and various environmental factors from 60 U.S. metropolitan areas [McDonald and Schwing, 1973]. For this exercise we shall model mortality rate given nitric oxides, sulfur dioxide, and hydrocarbons as inputs. This model is an extreme oversimplification as it combines all sources of mortality and does not adjust for crucial factors such as age and smoking. We use it to illustrate log transformations in regression.

(a) Create a scatter plot of mortality rate versus level of nitric oxides. Do you think a linear model will fit these data well? Fit the regression and evaluate a residual plot from the regression.

(b) Find an appropriate transformation that will result in data more appropriate for linear regression. Fit a regression to the transformed data and evaluate the new residual plot.

(c) Interpret the slope coefficient from the model you chose in the previous step.

(d) Now fit a model predicting mortality rate using levels of nitric oxides, sulfur dioxide, and hydrocarbons as inputs. Use appropriate transformations when appropriate. Plot the fitted regression model and interpret the coefficients.

(e) Cross-validate: split the data into two halves and refit the model you chose from the last step to the first half. Use the resulting model to predict the mortality rate using data from the second half. Discuss the result. (A “real” cross-validation often split the data into more, e.g., 20, subsets, and fit the model by leaving one subset out, and make predictions for the set-aside subset.)

(f) Interaction: use conditional plot to investigate potential interaction effects among the three predictors. If you have reason to believe that interaction effects are important, refit the model with these interactions and interpret the fitted model coefficients.

These steps are common for a statistical analysis of observational data. The first four steps are considered exploratory; step 5 verifies a model’s predictive capability. Step 6 is often ignored in many studies. In many cases, interaction is more interesting and more informative. Logarithmic transformation is frequently used, but its interpretation is rarely explained clearly in the literature. When explaining the models, you should interpret each model coefficients in plain English.

Write a short report on your findings.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"