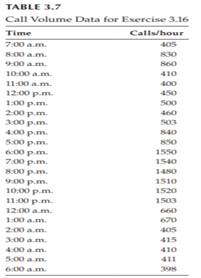
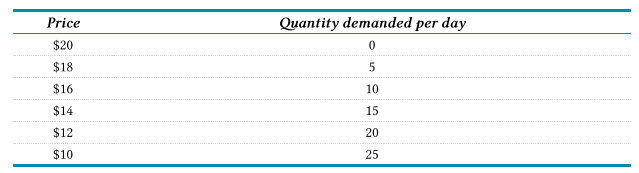
solution

/in /by

An M/M/1 queuing system has an arrival rate of 10 customers per hour. The average service time is 9 minutes.

a. What is the system utilization?

b. What is the average queue length?

c. What is the probability that there are more than 3 customers in the queue?

d. What is the probability that a customer will wait for more than 3 minutes for service?

Repeat Exercise 3.10 if there are only 10 customers allowed in the system.

Suppose the service time is not exponentially distributed for Exercise 3.8, but is instead log-normally distributed with μ = 8 and σ = 0.015. Use the P–K formulas to estimate the average waiting time in the queue.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

Consider a G/G/3 queuing system. Interarrival times are on average 5 minutes with a standard deviation of 6 minutes. Service times are on average 12 minutes with a standard deviation of 15 minutes. Use Equation 3.70 and Little’s law to determine average waiting time in the queue and average number of customers in the system.

Repeat Exercise 3.14 using the Whitt refinement given in Equations 3.73 through 3.80.

The call volume data for Figure 3.13 is given in Table 3.7. Develop and solve an integer programing formulation to find the minimum number of service agents to staff the offered load. An agent handles on average 10 calls per hour.

Consider a G/G/3 queuing system. Interarrival times are on average 5 minutes with a standard...

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

Consider the following demand schedule for umbrellas at a local store:

Consider the following demand schedule for umbrellas at a local store: a. Draw the demand curve for...

a. Draw the demand curve for umbrellas. Be sure to label the axes.

b. Suppose the price of umbrellas is $14. Indicate the area of market consumer surplus in your graph. Also indicate the area that represents the total amount that consumers spend on umbrellas.

c. Next, assume that Rebecca is willing to pay a maximum of $18 for an umbrella. What is Rebecca’s consumer surplus if she purchases an umbrella? Show her consumer surplus on your graph.

d. Another consumer, Andy, is willing to pay a maximum for $10 for an umbrella. What is his consumer surplus in this market?

e. If the demand schedule above represents demand on a normal summer day, what would you expect to happen to market consumer surplus if the forecast is for a heavy rainfall? Assume that the store does not raise its price. Draw a graph to support your answer.

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"

solution

/in /by

Suppose that the market equilibrium price for a basic medical check-up is $50, in a market in which there is no health insurance. To encourage more people to get a check-up, the local government mandates that the price of a check-up cannot be more than $40.

a. Is this a price floor or a price ceiling?

b. Draw a graph to illustrate the implementation of this government policy.

c. What happens to the number of check-ups in this market? Show this in your graph.

d. What happens to consumer surplus in this market? What happens to producer surplus? Show these changes on your graph.

e. Was the government’s policy successful? What has happened to social welfare? Show this in your graph.

f. Can you think of a different policy that would likely be more successful at encouraging more people to obtain check-ups?

g. Is this a typical market? Is there any reason to suppose that producers of health care would respond differently to price regulation than, say, producers of umbrellas? What does the producer’s responsiveness have to do with the cost of providing health care? What other factors might be involved?

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"