solution

/in /by

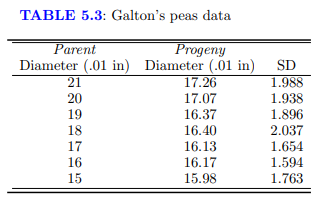
Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance of characteristics from one generation to the next. In a paper on “Typical Laws of Heredity,” delivered to the Royal Institution on February 9, 1877, Galton discussed some experiments on sweet peas. By comparing the sweet peas produced by parent plants to those produced by offspring plants, he could observe inheritance from one generation to the next. Galton categorized parent plants according to the typical diameter of the peas they produced. For seven size classes from 0.15 to 0.21 inches, he arranged for each of nine of his friends to grow 10 plants from seed in each size class; however, two of the crops were total failures. A summary of Galton’s data was published by Karl Pearson (see table 5.3 and the data file galtonpeas.txt). Only average diameters and standard deviation of the offspring peas are given by Pearson; sample sizes are unknown.

(a) Draw the scatter plot of Progeny versus Parent.

(b) Assuming that the standard deviations given are population values, compute the regression of Progeny on Parent and draw the fitted mean function on the scatter plot.

(c) Galton wanted to know if characteristics of the parent plant such as size were passed on to the offspring plants. In fitting the regression, a parameter value of Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-11 = 1 would correspond to perfect inheritance, while Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-11 Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-3 1 would suggest that the offspring are “reverting” towards “what may be roughly and perhaps fairly described as the average ancestral type” (the substitution of “regression” for “reversion” was probably due to Galton in 1885). Test the hypothesis that β1 = 1 versus the alternative that β1

(d) In his experiments, Galton took the average size of all peas produced by a plant to determine the size class of the parent plant. Yet for seeds to represent that plant and produce offspring, Galton chose seeds that were as close to the overall average size as possible. Thus, for a small plant, exceptionally large seed was chosen as a representative, while larger, more robust plants were represented by relatively smaller seeds. What effects would you expect these experimental biases to have on (1) estimation of the intercept and slope and (2) estimates of error?

table 5.3

Many of the ideas of regression first appeared in the work of Sir Francis Galton on the inheritance...-4

 
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"